本文是 XXVII POI (2019/2020 年度) 的中文翻译。今年受新冠疫情影响,Stage III 被取消了,因此只有 Stage I 和 Stage II 的题目。
Stage I
Najmniejsza wspólna wielokrotność (nww)
给出一个自然数 \(M\),找到一个区间 \([a,~b]\) 使得 \(M = \text{lcm}(a, a + 1, \dots, b)\),并且 \(a < b\)。
输入格式
输入数据第一行包含一个整数 \(z\),表示测试数据组数。对于每组测试数据:
第一行包含一个整数 \(M\),含义如题面所述。
输出格式
对于每组数据,如果不能找到一个合法的区间,输出 NIE。否则,输出两个正整数 \(a\) 和 \(b\)。如果存在多组解,找一个 \(a\) 最小的。如果还有多组解,找一个 \(b\) 最小的。
样例输入
3
12
504
17
样例输出
1 4
6 9
NIE
样例解释
对于第一个数据,\(12\) 是区间 \([2,4]\) 的最小公倍数,包含 \(2\),\(3\) 和 \(4\)。也是区间 \([1,4]\) 的最小公倍数,包含 \(1\),\(2\),\(3\) 和 \(4\)。其中后者的 \(a\) 更小。
附加样例参见 nww/nww*.in 和 nww/nww*.out:
- 附加样例 \(1\):\(5\) 组数据,\(M\) 依次为:\(5\),\(6\),\(7\),\(8\) 和 \(9\);
- 附加样例 \(2\):\(1\) 组数据,\(M\) 为 \(1\ 000\ 000\);
- 附加样例 \(3\):\(1\) 组数据,\(M\) 为 \(99\ 999\ 990\ 000\ 000\);
- 附加样例 \(4\):\(z = 10000\) ,\(M\) 为 \(500\ 001\ 500\ 001\ 000\ 001\) 和 \(500\ 001\ 500\ 001\ 000\ 000\) 交替出现。
数据范围与提示
| Subtask # | 额外限制 | 分值 |
|---|---|---|
| 1 | \(1 \le z \le 10, 1 \le M \le 1000\) | 18 |
| 2 | \(1 \le z \le 100, 1 \le M \le 10^9\) | 20 |
| 3 | \(1 \le z \le 100, 1 \le M \le 10^{18}\) | 20 |
| 4 | \(1 \le z \le 10000, 1 \le M \le 10^{18}\) | 42 |
Pisarze
给出一行波兰语文本,已知这段文本来自于以下三本书之一:
- Adama Mickiewicza 所著的 Pan Tadeusz。
- Henryka Sienkiewicza 所著 Quo Vadis。
- Bolesława Prusa 所著的 Lalka。
请你写一个程序判断这行文本来自于哪本书。
输入格式
输入数据第一行包含一个整数 \(T\),表示测试数据组数。对于每组测试数据:
第一行包含一段波兰语文本,由 \(10\) 到 \(2000\) 个单词组成。这一行的开头或者结尾都是一个完整的单词或者标点符号。
保证输入的所有文本长度之和不超过 \(2 \cdot 10^6\)。
输出格式
对于每组数据,输出 Mickiewicz,Prus 或者 Sienkiewicz,表示这行文本所在书的作者。
样例输入
3
Petroniusz obudzil sie zaledwie kolo...
Litwo! Ojczyzno moja! ty jestes jak...
W poczatkach roku 1878, kiedy swiat...
注意:样例输入并不完整,被截断了一部分。
样例输出
Sienkiewicz
Mickiewicz
Prus
数据范围与提示
这题的代码长度不能超过 \(10\) KB。
这是一个数据分析题,你的程序不需要准确的识别每组数据。评分标准如下:
- 令 \(T\) 是测试数据组数。
- 令 \(P\) 是选手程序识别对的数据组数。
- 如果 \(P \ge 0.9 \cdot T\),那么选手会获得 \(100\%\) 的分数。
- 如果 \(P \le \frac{T}{3}\),选手会获得 \(0 \%\) 的分数。
- 否则,选手获得的分数为 \(100 \cdot \frac{P- \frac{T}{3}}{0.9 \cdot T - \frac{T}{3}} \%\)。
每个测试数据的文本来自于提供的文本,同时还附赠了一个脚本 pistestgen.py,可以从这里下载。用命令 python3 pistestgen.py subtask name directory [seed] 即可生成一组数据,其中:
subtask是子任务编号,一个从 \(1\) 到 \(4\) 的整数。name是测试数据的名字,这个脚本会生成name.in和name.out这两个文件。directory是包含这三本书的文件夹路径。seed是可以不加的字符串,用于生成同一组数据(两次程序如果seed值是一样,那么生成的数据也是一样的)。
所有的测试数据保证也是通过这个程序生成的。
| Subtask # | 额外限制 | 分值 |
|---|---|---|
| 1 | \(T \le 100\),每行包含 \(500\) 到 \(2000\) 个单词 | 20 |
| 2 | \(T \le 1000\),每行都是由完整的句子组成 | 20 |
| 3 | \(T \le 1000\),每行包含 \(30\) 到 \(80\) 个单词 | 30 |
| 4 | \(T \le 1000\) | 30 |
Pomniejszenie
给出两个数字串 \(A\) 和 \(B\),保证 \(A \ge B\)。你可以修改 \(A\) 里面恰好 \(k\) 个数字,求出比 \(B\) 小的最大数字。
输入格式
输入数据第一行包含一个整数 \(t\),表示测试数据组数。对于每组测试数据:
第一行包含三个非负整数 \(A\),\(B\) 和 \(k\)。保证 \(A\) 和 \(B\) 的长度是一样的,并且可能有前导零。\(k\) 是一个正整数,并且不会超过 \(A\) 和 \(B\) 的长度。
输出格式
对于每组数据,输出一个满足下面条件的整数 \(C\):
- \(C\) 的长度必须和 \(A\) 以及 \(B\) 的一样,可以包含前导零。
- \(C\) 是由 \(A\) 恰好修改了 \(k\) 个字符得到。
- \(C\) 要尽可能的大,并且 \(C\) 要小于 \(B\)。
如果不存在满足按上面条件的 \(C\),请输出\(-1\)。
样例输入
4
555 333 1
0555 0551 3
0555 0333 4
9 9 1
样例输出
255
0499
-1
8
附加样例参见 pom/pom*.in 和 pom/pom*.out:
- 附加样例 \(1\):\( t = 100\);\(A\) 依次是 \(20\ 000, 20\ 001, \dots\);\(B\) 一直是 \(20\ 000\);\(k=1\);
- 附加样例 \(2\):\(t = 100\);对于每组数据 \( n = 5000\),并且 \(A\) 和 \(B\) 里仅包含数字
9;\(k\) 依次是 \(4901, \dots, 5000\); - 附加样例 \(3\):\(t = 100\);对于每组数据 \( n = 10^5\),并且 \(A\) 里包含数字
9,\(B\) 里仅包含数字2;\(k\) 依次是 \(1, \dots, 100\)。
数据范围与提示
令 \(n\) 是数字串 \(A\) 和 \(B\) 的长度,保证对于所有数据有 \(1 \le t \le 100\)。
| Subtask # | 限制 | 分值 |
|---|---|---|
| 1 | \(1 \le n \le 5\) | 18 |
| 2 | \(1 \le n \le 5000\) | 20 |
| 3 | \(1 \le n \le 10^5, k=1\) | 20 |
| 4 | \(1 \le n \le 10^5\) | 42 |
Przedszkole
有一个 \(n\) 个点 \(m\) 条边的无向图,每个点从 \(1\) 到 \(n\) 编号。你有 \(k\) 种颜色,要给每个点染色,使得有边相连的两个点颜色不一样。求出染色方案数,对 \(10^9+7\) 取模。
输入格式
第一行包含 \(3\) 个整数 \(n\),\(m\) 和 \(z\),表示图中点个数,边条数和询问个数。
接下来 \(m\) 行,每行包含两个整数 \(a_i\) 和 \(b_i\),表示点 \(a_i\) 和 \(b_i\) 之间有一条边相连。保证不会有重边和自环。
接下来 \(z\) 行,每行包含一个整数 \(k_i\),表示你有 \(k_i\) 种颜色。
输出格式
对于每组数据,输出你有 \(k_i\) 种颜色时的染色方案数,对 \(10^9+7\) 取模。
样例输入
4 4 1
1 2
2 3
1 3
3 4
3
样例输出
12
附加样例参见 prz/prz*.in 和 prz/prz*.out:
- 附加样例 \(1\):\(n=5,m=10\),两个询问 \(k \in \{5, 6\}\);
- 附加样例 \(2\):\(n=11,m=40\),一个询问 \(k=15\);
- 附加样例 \(3\):\(n=100,m=15\),\(5\) 个询问,\(k\) 从 \([10, 100]\) 里面随机;
- 附加样例 \(4\):\(n=100,m=100\),所有点构成了一个环;三个询问 \(k \in \{5, 10, 15\}\)。
数据范围与提示
对于 \(100\%\) 的数据,\(1 \le n \le 10^5, 0 \le m \le \min(10^5, n(n-1)/2), 1 \le z \le 1000, 1 \le a_i, b_i \le n, 1 \le k_i \le 10^9\)。
| Subtask # | 额外限制 | 分值 |
|---|---|---|
| 1 | \(n \le 8, k \le 8, z \le 50\) | \(8\) |
| 2 | \(n \le 15\) | \(26\) |
| 3 | \(m \le 24\) | \(33 \) |
| 4 | 每个点恰好有两条边和它相连 | \(33\) |
Układ scalony
有一个 \(n \cdot m\) 个点排成 \(n\) 行 \(m\) 列,其中第 \(i\) 行第 \(j\) 列的坐标为 \((i, j)\)。对于两个点 \((x_1,y_1)\) 和 \((x_2,y_2)\),如果 \(|x_1-x_2| + |y_1-y_2|=1\),那么它们之间有一条边相连。
给定一个整数 \(k\),你需要找到这个图的一个生成树,使得它的直径上恰好有 \(k\) 条边。
输入格式
输入仅一行包含三个整数 \(n\),\(m\) 和 \(k\)。
输出格式
如果不存在这样的生成树,输出 NIE。否则,在第一行输出 TAK。接下来 \(nm-1\) 行,每行包含 \(4\) 个整数 \(i_1,j_1,i_2,j_2\) (\(1 \le i_1, i_2 \le n, 1 \le j_1, j_2 \le m\)),表示点 \((i_1,j_1)\) 和点 \((i_2,j_2)\) 之间有边相连。如果有多组解,输出任意一组即可。
样例输入 1
2 3 4
样例输出 1
TAK
1 1 1 2
1 1 2 1
1 2 2 2
2 3 2 2
1 2 1 3
样例解释 1
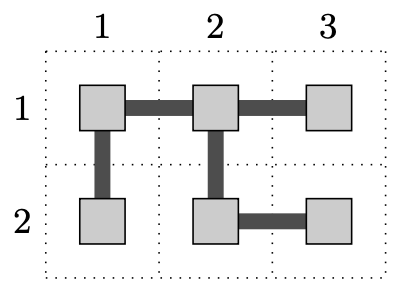
样例输入 2
2 3 1
样例输出 2
NIE
附加样例参见 ukl/ukl*.in 和 ukl/ukl*.out:
- 附加样例 \(1\):\(n=2,m=3,k=3\);
- 附加样例 \(2\):\(n=1,m=10,k=10\);
- 附加样例 \(3\):\(n=1000,m=1000,k=999\ 999\)。
数据范围与提示
对于 \(100\%\) 的数据,\(1 \le n, m \le 1000, 0 \le k \le 10^6\)。
| Subtask # | 限制 | 分值 |
|---|---|---|
| 1 | \(n,m\le 6\) | 20 |
| 2 | \(n \le 3, m \le 1000\) | 20 |
| 3 | \(n,m \le 1000\),\(n \cdot m\) 是奇数 | 30 |
| 4 | \(n,m \le 1000\),\(n \cdot m\) 是偶数 | 30 |
Stage II
Day 0
Wakacje Bajtazara (wak)
给出一棵 \(n\) 个点的树,第 \(i\) 个点有个权值 \(w_i\)。现在你需要一条长度为 \(2k-1\) 的路径 \(p_1,p_2,\dots,p_{2k-1}\),使得:
- \(p_i\) 和 \(p_{i+1}\) 在树上相邻
- \(p_1,p_3,p_5,\dots,p_{2k-1}\) 互不相同
- \(w_{p_1}+w_{p_3} + \dots + w_{p_{2k-1}}\) 最大
输入格式
第一行一个整数 \(n\) (\(1 \le n \le 10^6\)),表示树上节点个数。
第二行 \(n\) 个整数 \(w_1,w_2,\dots,w_n\) (\(1 \le w_i \le 10^6\)),表示每个点的权值
接下来 \(n-1\) 行,每行两个整数 \(a_i\) 和 \(b_i\) (\(1 \le a_i, b_i \le n\)),表示树上一条边。
输出格式
第一行输出一个整数表示最大权值。第二行输出一个整数表示 \(k\) 的大小。第三行输出 \(p_1,p_2,\dots,p_{2k-1}\)。如果有多个方案,输出任意一个即可。
样例输入
8
3 8 5 4 1 2 1 1
1 2
2 3
2 4
5 4
4 6
7 6
8 7
样例输出
13
4
3 2 1 2 4 6 7
Day 1
Drzewo czwórkowe (czw)
有一个 \(2^m \times 2^m\) 的黑白格子,现在用一个递归定义的字符串来描述这个格子。
- 如果整个格子都是白色的,用一个
0来标记 - 如果整个格子都是黑色的,用一个
1来标记 - 否则,先用
4来标记,接下来对应 \(4\) 个 \(2^{m-1} \times 2^{m-1}\) 的格子描述,依次为左上角,右上角,左下角,右下角的格子。
现在给出 \(m\) 和用于描述这个格子的字符串。求出这个格子里面黑色连通块的个数和面积最大的黑色连通块。面积对 \(10^9 + 7\) 取模。
输入格式
第一行包含一个整数 \(m\) (\(1 \le m \le 10^9\)),表示格子的大小。
第二行包含一个仅包含 0、1 和 4 的字符串,对应了这个格子的描述,长度不超过 \(10^6\)。
输出格式
第一行输出黑色连通块的数目。第二行输出面积最大的黑色连通块,对 \(10^9+7\) 取模。
样例输入
3
404004111014001410011
样例输出
2
24
Wielki Upadek (wie)
有 \(n\) 个多米诺骨牌,第 \(i\) 个立在了位置 \(x_i\) 处,高度为 \(h_i\)。现在又给出 \(N_1\) 个高度为 \(H_1\) 和 \(N_2\) 个高度为 \(H_2\) 个多米诺骨牌。保证要么 \(H_1\) 是 \(H_2\) 的约数,要么 \(H_2\) 是 \(H_1\) 的约数。并且 \(H_1\) 和 \(H_2\) 都小于之前的多米诺骨牌高度,也就是说 \(\max(H_1,H_2) < \min(h_1,h_2,\dots,h_n)\)。
你可以任意放置这 \(N_1+N_2\) 个多米诺骨牌,然后最后选个多米诺骨牌往左或者往右推。求出最多能够推倒多少多米诺骨牌。
如果位置 \(x\) 和 \(y\) (\(x < y\)) 有个骨牌,高度分别为 \(h_1\) 和 \(h_2\)。如果在 \(x\) 往右推并且 \(x+h_1 \ge y\),那么在 \(y\) 的骨牌也会被推倒;如果在 \(y\) 往左推并且 \(y-h_2 \le x\),那么在 \(x\) 的骨牌也会被推倒。
输入格式
第一行包含一个整数 \(n\) (\(1 \le n \le 200000\)),表示一开始放置好的多米诺骨牌个数。
接下来 \(n\) 行,每行包含一个整数 \(x_i\) 和 \(h_i\) (\(0 \le x_i \le 10^{18}, 1 \le h_i \le 2000000\)),表示第 \(i\) 个多米诺骨牌放在了位置 \(x_i\) 处,高度为 \(h_i\)。
接下来一行包含四个整数 \(N_1\),\(H_1\),\(N_2\) 和 \(H_2\) (\(0 \le N_1, N_2 \le 10^{18}, 1 \le H_1, H_2 \le 10^6\)),含义如题所述。
输出格式
输出一行表示最多能推倒的多米诺骨牌数目。
样例输入
3
1 5
10 6
20 7
1 4 2 1
样例输出
5
Day 2
Trudny dylemat przedszkolanina (tru)
给出一个正整数 \(n\),求出两个不超过 \(n\) 的正整数 \(x\) 和 \(y\),使得集合 \(\{d: d \mid x \text{ or } d \mid y \}\) 的大小最大。
输入格式
第一行包含一个整数 \(n\) (\(1 \le n \le 10^{16}\))
输出格式
第一行输出集合的大小。第二行输出两个整数 \(x\) 和 \(y\),表示一个解。如果有多组解,输出任意一个即可。
样例输入
15
样例输出
8
12 10
Marudny Bajtazar (mar)
有一个长度为 \(n\) 的 01 串。有 \(m\) 个操作,每次翻转位置 \(a_i\) 的字符,把 0 变成 1 或者把 1 变成 0。每次操作后,找出最短的不作为子串出现的 01 串的长度。
\(1 \le n \le 10^5, 0 \le m \le 10^4\)
输入格式
第一行包含两个整数 \(n\) 和 \(m\) (\(1 \le n \le 10^5, 0 \le m \le 10^4\)),表示字符串长度和操作个数。
第二行包含一个长度为 \(n\) 的 01 串。
接下来 \(m\) 行,每行包含一个整数 \(a_i\) (\(1 \le a_i \le n\)),表示需要翻转的位置。
输出格式
输出 \(m+1\) 行,第 \(i\) 行表示第 \(i-1\) 次操作后的答案。第一行表示没有任何操作时的答案。
样例输入
6 2
001010
6
2
样例输出
2
3
2